可持久化线段树(主席树)
前置芝士 : 线段树,离散化(部分题目需要)
主席树是一种以线段树为基础的可以快速查询区间第k小(大)的数据结构,其中可持久化的意思就是对于每次修改,我们都将结果保存下来,然后你可以随时查询修改之前任意一次操作时所对应的线段树,类似于git,可以查看历史版本。为了实现这一功能,容易想到的是暴力建树,即对于每次操作都重新建立一颗线段树,但这样做时间空间肯定会炸的稀里哗啦。于是我们换个角度想,考虑到对于每次修改,实际变动的节点只是少数,如下图: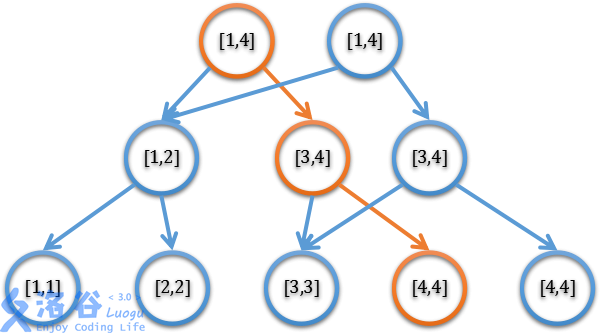
假如现在正在进行第x次操作,我们对原序列第四个点进行修改,其中橙色节点是第x-1次操作对应的线段树的节点,而其右边是第x次操作新建立的线段树节点。这里若修改第4个点,则只有橙色的节点维护的信息发生了变动,而其他节点都保持不变,考虑到这一特点,在每次修改后,我们只需要创建与受到影响的节点(橙色节点)相对应的节点(橙色节点右边的节点),然后让他们共用那些没有被影响的节点,这样一来,便可以很快的建好第x次操作所对应的线段树,并且极大节约了空间。(与普通线段树不同的是,节点的左右儿子编号并不能被计算出来,需要另行记录)
下面我们通过一道例题具体实现下,此题需进行离散化 可参考这篇博客的方法二
题意
给定 n 个整数构成的序列,将对于指定的闭区间查询其区间内的第 k 小值。
输入格式
第一行包含两个正整数 n,mn,m,分别表示序列的长度和查询的个数。
第二行包含 nn 个整数,表示这个序列各项的数字。
接下来 mm 行每行包含三个整数 l, r, kl,r,k , 表示查询区间 [l, r][l,r] 内的第 kk 小值。
输出格式
输出包含 mm 行,每行一个整数,依次表示每一次查询的结果
数据范围
1 <= n,m <= 2*10^5 数列中的所有数绝对值都不超过10^9
这是一道板子题,我将结合代码用注释解释
Code
#include<cstdio>
#include<algorithm>
#define maxn 200005
using std::sort;
using std::unique;
using std::lower_bound;
int n,m,cnt,p,k,l,r;
int cl[maxn<<5],cr[maxn<<5],sum[maxn<<5];
//cl[i],cr[i],sun[i]分别为i号节点的左孩子序号,右孩子序号,i号节点管理的区间和
int rt[maxn],a[maxn],b[maxn];
//rt[i]是第i颗线段树的根节点号码,a,b分别是原数组和其副本
int change(int u,int l,int r){ //u是与现在访问的节点相对应的上一颗数的节点号码,l,r是该号码所管理的区间
int t = ++cnt; //t是新建立的节点号码
cl[t] = cl[u],cr[t] = cr[u],sum[t] = sum[u]+1; //先让t号节点继承上一颗线段树与之对应的节点的信息
if(l == r) //该节点没有孩子了,结束更新
return t;
int mid = (l+r)>>1;
if(p <= mid) //变动的节点在左子树,递归进入左子树创立新节点
cl[t] = change(cl[u],l,mid);
else
cr[t] = change(cr[u],mid+1,r);
return t; //返回这次创立的节点序号
}
int query(int fu,int u,int l,int r,int k){ //返回第k小的数离散化后的rank
if(l == r)
return l;
int mid = (l+r)>>1,num = sum[cl[u]]-sum[cl[fu]]; //主席树是可减的,这里实际模拟下就很清楚了
if(num >= k)
return query(cl[fu],cl[u],l,mid,k);
else
return query(cr[fu],cr[u],mid+1,r,k-num);
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1;i <= n;i++){
scanf("%d",&a[i]);
b[i] = a[i]; //因为要进行离散化,而之后还要用该数组的值,所以创建副本
}
// 下面是离散化操作
sort(b+1,b+1+n);
int len = unique(b+1,b+1+n)-b-1;
for(int i = 1;i <= n;i++){ //对原数组下标1-i的数建一颗线段树(也就是一个版本),一共会建立n颗线段树
p = lower_bound(b+1,b+1+len,a[i])-b;
rt[i] = change(rt[i-1],1,len); //change函数会创建新节点,同时返回新创建的节点标号
}
while(m--){
scanf("%d%d%d",&l,&r,&k);
int t = query(rt[l-1],rt[r],1,len,k);
printf("%d\n",b[t]);
}
return 0;
}下面放两道主席树的其他类型题目:
洛谷 p3919
洛谷 p3402